MATH172000--程式設計二

Q3: All Pairs Shortest Path

作業資訊

檔名必須為「q3_你的學號.py」，例如 q3_9962816.py

題目敘述

矩陣乘法的定義是：假設 A 是 m-by-p 矩陣，B是 p-by-n 矩陣，則 A * B 所得之 C 矩陣是 m-by-n，且：

但今天，我們要算的是兩個矩陣之間的一種新運算 ⊕，D = A ⊕ B，定義如下：

本題要請你撰寫一個函式 all_pairs_shortest_path，輸入是一個方陣 M 跟一個正整數 k，請大家計算出 M 矩陣對自己做 ⊕ 運算 k 次的結果。例如 k = 2 就計算 M ⊕ M，k = 3 即計算 M ⊕ M ⊕ M。

輸入說明

第一個參數是一個 numpy array，代表前述的方陣 M，且內容都是整數。第二個參數是一個 2 以上的正整數，代表前述的 k。

輸出說明

一個 numpy array，代表運算出的結果。

Sample Input

[[1, 2], [3, 4]], 5

Sample Output

[[5, 6], [7, 8]]

提示與注意事項

測資只有一組。
本題允許使用 numpy。

程式架構範例如下，建議只修改標為 pass 的地方以及「if __name__ == '__main__':」區塊的內容，否則若影響自動批改時，可能會有折扣：

import numpy as np


def all_pairs_shortest_path(mat, k):
	pass


if __name__ == '__main__':
	mat = np.array([[1, 2], [3, 4]])
	k = 5
	print(all_pairs_shortest_path(mat, k))

關於本題

※以下資料跟本題代表的意義有關，對於解題不一定有幫助，若有興趣可以等寫完作業以後再看。

尋找最短路徑在各個領域都是很常見的問題，如三角套利等等。本題所定義的計算，可以很快的解出所有節點之間最短的路徑。例如下圖是一張四個城鎮的地圖簡圖，包含城鎮之間的道路與其長度：

如果要計算兩兩城市之間的最短距離，我們可以先把互相有直接聯繫道路的城市放在矩陣裡面，當然自己到自己的距離是 0，而沒有直接道路連接的城鎮之間，距離就是無窮大：

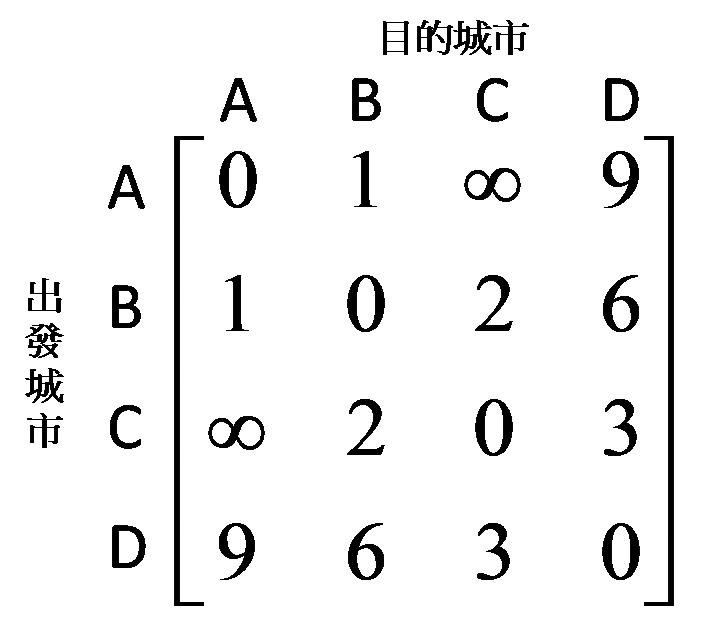
接下來我們計算「如果可以經過 1 個其他城市」時，兩兩城市的最短路徑。即 A 到 C 雖然沒有直接連接，但是若允許經過 1 個其他城市，則存在路徑 A -> D -> C 或是 A -> B -> C。因此 A -> C 之間，可經過 1 個其他城市的最短距離，就是以下四種方法中最小的：

A -> A 的距離 + A -> C 的距離
A -> B 的距離 + B -> C 的距離
A -> C 的距離 + C -> C 的距離
A -> D 的距離 + D -> C 的距離

因此如果拿上圖矩陣進行 ⊕ 運算，得到新的矩陣就是允許通過 1 個其他城市條件下，兩兩城市的最短路徑。同理，若允許通過 2 個其他城市，只需要計算上圖矩陣的 3 次方即可。此外，因為距離都是正數，因此若次方大於 k - 1 時，該矩陣將不會繼續變化。