LAPACK 是 Linear Algebra PACKage 的縮寫，它是一個以 Fortran 語言寫成的函式庫。 本篇的目標，是要以矩陣相乘等常見的函式為例，來介紹 LAPACK 的使用。 由於自己下載原始碼，並編譯出函式庫的步驟比較繁瑣， 所以這裡提供了事先編譯好的 lapack.rar 讓各位下載， 請解壓縮後把它們放在同一個資料夾，例如"C:\lapack"。 (如果對自行編譯有需要的話，可以檢視本網頁的原始碼，裡面用註解的方式記錄了一些比較重要的步驟。)

接著，我們要讓 Code::Blocks 知道函式庫放在哪裡。請先選擇 Settings → Compiler，應該會出現這個畫面：

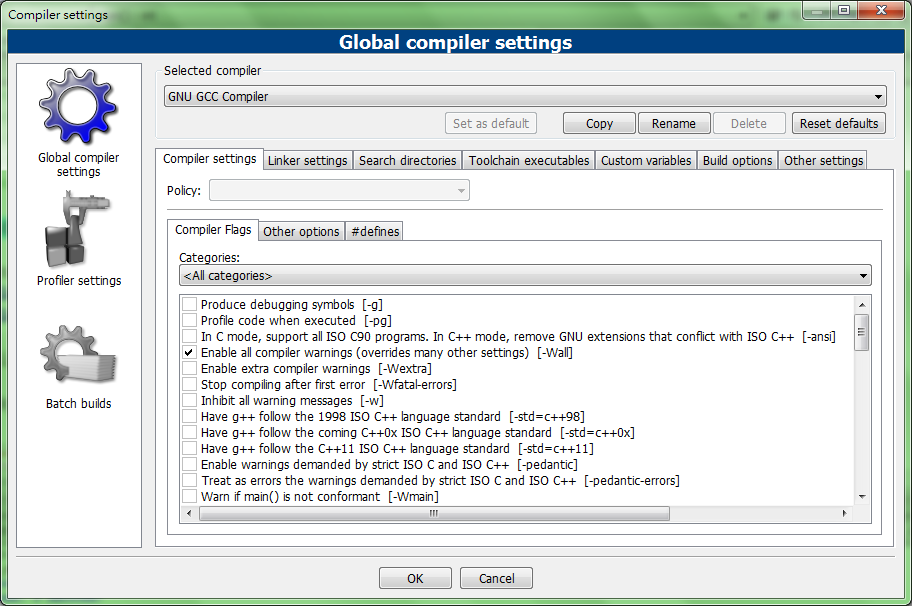
再來，請找到 linker settings 這個分頁，把三個 *.a 的函示庫加入路徑中

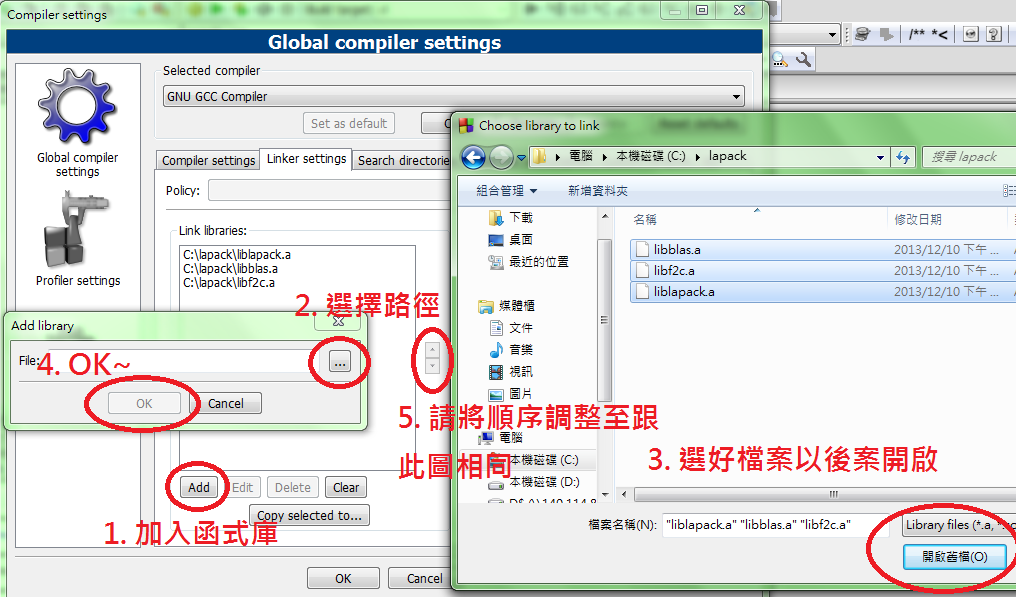
下一步，請找到 Search directories 這個分頁， 加入 C:\lapack 或你放置的其他路徑，才能讓 Code::Blocks 找到相對應的 *.h 檔案。

現在，你可以先試著編譯與執行這個程式：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <f2c.h>
#include <clapack.h>

void matrixDisplay(double mat[], int m, int n){
    int i, j;
    for(i=0;i<m;i++){
        for(j=0;j<n;j++){
            printf("%.0f ",mat[i*n+j]);
        }
		printf("\n");
    }
}

int main()
{
    int n;
    double *A,*B,*C;
    double alpha=1.0, beta=0.0;
    char trans='t';
    int i,j;

    clock_t tic,toc;

    /* space allocation */
    n = 2;
    A = (double*)malloc(n*n*sizeof(double));
    B = (double*)malloc(n*n*sizeof(double));
    C = (double*)malloc(n*n*sizeof(double));

    /* value generation/initialization */
    srand(time(NULL));
    j = n*n;
    for(i=0; i<j; i++){
        A[i] = rand()%5+1;
        B[i] = rand()%5+1;
        C[i] = 0.0;
    }

    /* computation */
    tic = clock();
    dgemm_(&trans, &trans, &n, &n, &n,&alpha, A, &n, B, &n,&beta, C, &n);
    toc = clock();
    printf("%.4f\n",(double)(toc-tic)/CLOCKS_PER_SEC);

    /* display */
    printf("==================\n");
    matrixDisplay(A, n, n);
    printf("==================\n");
    matrixDisplay(B, n, n);
    printf("==================\n");
    matrixDisplay(C, n, n);
    printf("==================\n");
	
    free(A);
    free(B);
    free(C);
    return 0;
}

這個程式會亂數產生兩個 2-by-2 的矩陣，然後利用 LAPACK 計算矩陣乘積。 首先，要使用 LAPACK 的功能，必須含括 f2c.h 和 clapack.h。 time.h 則是計時用，在此範例中，由於矩陣很小，所以時間不明顯。 再來，對於矩陣的部分，我們必須使用一維矩陣來存放資料，然後自行對應至二維。

然後是最重要的，呼叫 LAPACK 的部分，我們使用的是「dgemm_」這個函式。 它會幫你計算這個式子：

C = α*op(A)*op(B) + β*C
其中，op() 代表矩陣要轉置或者不要轉置，由輸入參數決定。 命名的規則稍後來說明，我們先介紹參數如下， 完整的說明可以參考這裡：

• transA: 控制 A 矩陣是否轉置；若值為'N'或'n'時代表不轉置，'T'或't'時代表轉置。
• transB: 控制 B 矩陣是否轉置；若值為'N'或'n'時代表不轉置，'T'或't'時代表轉置。
• m: op(A) 矩陣的 rows 的個數。
• n: op(B) 矩陣的 columns 的個數。
• k: op(A) 矩陣的 columns 的個數，即 op(B) 矩陣的 rows 的個數。
• α: 如前述式子。
• A: A 矩陣。
• LDA: A 未轉置時為 m，轉置時為 k。
• B: B 矩陣。
• LDB: B 未轉置時為 k，轉置時為 n。
• β: 如前述式子。
• C: C 矩陣。
• LDC: 與 n 同值。

所以，如果要進行兩個方陣 A 和 B 的相乘，則矩陣大小皆為 n，α 為 1，β 為 0。 在 trans 的部分，由於在 C 語言裡面，把二維放成一維時，習慣一個 row 接一個 row 放(稱為 row-major)； 而 LAPACK 使用的 Fortran 語言，習慣一個 column 接一個 column 放(稱為 column-major)， 所以 trans 在此處皆使用 't'。 當然，輸出的 C 矩陣是 column-major，而此處在印出前並沒有特別轉換，所以你會覺得看到的矩陣方向不太對。 另外，此函式庫需要傳入記憶體位置，所以若是非指標型態的變數，記得加上「&」。

接下來我們介紹命名規則。由於早期的 Fortran 在函式名稱的字數上有些限制， 因此有規則如下(少數特例本篇不介紹)：

• 第一個字母代表變數類型，LAPACK 有四種變數類型：
• single (s): 單精度浮點數，即 C 語言的 float。
• double (d): 倍精度浮點數，即 C 語言的 double。
• complex (c): 單精度複數，即 C 語言的 struct { float r, i; }。
• doublecomplex (z): 單精度浮點數，即 C 語言的 struct { double r, i; }。
• 再來的兩個字母代表矩陣的樣子，部分舉例如下：
• GE: general，一般的矩陣。
• DI: diagonal，只有對角線的矩陣。
• SY: symmetric，對稱矩陣
• 最後的幾個字代表要進行的運算，例如：
• TRF: 三角化，即 LU 分解。
• TRS: 解 AX=B，其中 A 是 xyyTRF 計算出的三角矩陣。
• MM: 矩陣乘積。

因為 LAPACK 提供的函式很多，本篇就不一一介紹。 以下示範 double 類型的 LU 分解的範例，需要使用的函式是「dgetrf_」，參數說明如下：

• m: A 矩陣的 rows 的個數。
• n: A 矩陣的 columns 的個數。
• A: A 矩陣。函式結束時，會將 L 和 U 存在這裡。
• LDA: 至少要是 m。
• ipiv: 整數陣列，會把 row 交換的過程存下來，第 i 個 row 會和第 ipiv(i) 個 row 交換。
• info: 整數，代表計算結果。
• 0: 成功。
• <0: 值為 -i 時代表第 i 個參數有非法值。
• >0: 值為 -i 時代表 U(i,i) 為 0。

完整程式如下：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <f2c.h>
#include <clapack.h>

void matrixDisplay(double mat[], int m, int n){
    int i, j;
    for(i=0;i<m;i++){
        for(j=0;j<n;j++){
            printf("%.0f ",mat[i*n+j]);
        }
		printf("\n");
    }
}

int main()
{
    int n, *ipiv;
    double *A;
    int i, j, info;
	
    /* space allocation */
    n = 3;
    A = (double*)malloc(n*n*sizeof(double));
	ipiv = (int*)malloc(n*sizeof(int));

    /* value generation/initialization */
    srand(time(NULL));
    j = n*n;
    for(i=0; i<j; i++){
        A[i] = rand()%5+1;
    }
	
	matrixDisplay(A, n, n);
    dgetrf_(&n, &n, A, &n, ipiv, &info);
    matrixDisplay(A, n, n);
	
    free(A);

    return 0;
}