動態規劃(Dynamic Programming)是一個基於填表的計算方法。Programming 是求取最佳解的意思，所以 Dynamic Programming 就是動態的求得目前的最佳解。如果你面對的問題，是可以透過把問題切割、合併來解決，而且切割出的小問題會重複時，就很適合利用動態規劃來解決。例如計算費氏數列的遞迴版本，在計算 fibo(5) 時，會呼叫 fibo(4) 和 fibo(3)，而因為 fibo(4) 會呼叫 fibo(3) 和 fibo(2)，所以 fibo(3) 就屬於會重複計算的狀況。其實，在更前面的迴圈篇章看過的費氏數列範例，其實已經是動態規劃的版本。底下將介紹其他幾個可以用動態規劃解決的問題。

首先是「最長共同子序列(longest common subsequence)」問題。子序列的意思是，從原始的序列當中去掉任意個數的元素，則新的序列就是原始序列的子序列。而最長共同子序列，就是求取一個子序列，其能同時是兩個序列的子序列，並且長度要是最長的。你也可以把這個問題想成連連看，我們要把兩個字串中一樣的字母連起來，要盡可能的連出多一點線條，但是不能交叉；而我們的目標，就是在給定兩個序列的情況下，找出最多能連幾條線，以及若有需要時，要回答連線方式。如下圖：

那麼要如何求解呢？首先，假設我們已知兩個字串，例如 'abc' 和 'abcd' 的最佳連線方法，則當兩個字串各多加入一個字母時，有兩種情況。第一種情況是，如果新加進來的兩個字母是相同的，則很顯然地，若讓那兩個字母直接連線，一定會是最佳解（之一）：

第二種情況則是，如果新加進來的兩個字母不一樣，則至少有一個字母不會被配對，相當於比較以下兩種情況誰比較好：

因此，若有一個表格 D，其中的 Di-1, j-1 代表字串 A 的前 i - 1 個字和字串 B 的前 j - 1 個字的最佳連線方式的話，則 Di, j 可以表示成下列三個式子當中的最大值：

當然，如果其中一個字串，例如 A 只有一個字，則應該變成下列兩個式子的最大值（字串 B 只有一個字的情況請依此類推）：

字串 A 和 B 都只有一個字時，則可以直接判斷他們是否相等，若是則為 D1, 1 為 1，否則為 0。

整體的範例如下。其中，在實作上，我們通常還會把 index 0 的 row 和 column 「浪費」掉，來讓邊界狀況（任何一個字串只有一個字的）的程式寫法比較簡潔：

str_a = 'IVVSVSTN'
str_b = 'IVIVVVSVAVTN'
d = [[0 for _ in range(len(str_b)+1)] for _ in range(len(str_a)+1)]
for i in range(1, len(str_a)+1):
	for j in range(len(str_b)+1):
		if str_a[i-1] == str_b[j-1]:
			d[i][j] = d[i-1][j-1] + 1
		else:
			d[i][j] = max(d[i-1][j], d[i][j-1])
print(d[-1][-1])

上述的範例只能求取最長共同序列的長度。如果你希望找出該序列的話，則除了求取最大值外，有需要把產生最大值的方向記錄下來，並在最後回溯回去：

str_a = 'IVVSVSTN'
str_b = 'IVIVVVSVAVTN'
d = [[0 for _ in range(len(str_b)+1)] for _ in range(len(str_a)+1)]
path = [[0 for _ in range(len(str_b)+1)] for _ in range(len(str_a)+1)]
for i in range(1, len(str_a)+1):
	for j in range(len(str_b)+1):
		if str_a[i-1] == str_b[j-1]:
			d[i][j] = d[i-1][j-1] + 1
			path[i][j] = 'upleft'
		elif d[i-1][j] >= d[i][j-1]:
			d[i][j] = d[i-1][j]
			path[i][j] = 'up'
		else:
			d[i][j] = d[i][j-1]
			path[i][j] = 'left'
print(d[-1][-1])

i = len(str_a)
j = len(str_b)
seq = ''
while path[i][j] != 0:
	if path[i][j] == 'upleft':
		seq = str_a[i-1] + seq
		i -= 1
		j -= 1
	elif path[i][j] == 'up':
		i -= 1
	else:
		j -= 1
print(seq)

下一個要介紹的是 0-1 背包問題。這個問題是說，有一個尋寶人，發現了 n 個寶物，每個寶物 j 的價值是 Pj，重量則是 Wj，尋寶人希望在有承重限制 W 的背包裡，裝下價值總和最高的寶物。在這個問題裡，如果寶物可以分割，那很明顯就從單價最高的寶物先拿再說； 但是 0-1 背包問題討論的，是寶物不可分割的狀況，所以情況會變得比較複雜。

要解決這個問題，我們一樣來填一張表格，其中 Di, j 代表「在承重限制是 i 的狀況下，只考慮前 j 樣物品」的最佳解。而對每一樣物品來說，都分成要拿與不拿兩種狀況； 如果要拿，就是取得其價值，但是總承重量減少；如果不拿，則其已獲得的總價值跟剩餘的承重限制都不變。因此，若第 j 個物品：

以下以實際的數字來說明。假設我們共有五樣物品，背包限裝 15 單位重：

物品價值重量
A412
B22
C21
D11
E104

則我們可以開出一個 (15 + 1) x (5 + 1) 的表格，並撰寫如下程式，就可以獲得最佳解：

price = [4, 2, 2, 1, 10]
weight = [12, 2, 1, 1, 4]
w_limit = 15
d = [[0 for _ in range(len(price)+1)] for _ in range(w_limit+1)]
for i in range(1, w_limit+1):
	for j in range(1, len(price)+1):
		if i - weight[j-1] < 0:
			d[i][j] = d[i][j-1]
		else:
			d[i][j] = max(d[i][j-1], d[i-weight[j-1]][j-1] + price[j-1])
print(d[-1][-1])

再來要介紹的問題叫做「矩陣鏈乘積(Matrix Chain Multiplication)」。先想像一下有三個矩陣 A, B, C 要相乘，你要用 (AB)C 還是 A(BC)的順序來乘呢？假設它們的維度分別是 5-by-5, 5-by-3, 3-by-1，則 (AB)C 的順序，需要 5 * 5 * 3 + 5 * 3 * 1 = 90 次乘法運算；而 A(BC) 的順序，則只需要 5 * 3 * 1 + 5 * 5 * 1 = 40 次乘法運算。當矩陣的數量一多的時候，順序的差別就會更明顯，而要找出好的順序，就成了一個重要的問題。這次我們用由上往下的角度來思考：

假設有 ABCDE 五個矩陣相乘，你的第一刀要切在哪裡？

如果是 (A)(BCDE) 的切法，則你需要知道 BCDE 的最少乘法次數；如果是 (AB)(CDE) 的切法，則你分別需要知道 AB 的最少乘法次數，以及 CDE 的最少乘法次數；如果是 (ABC)(DE) 的切法，則你分別需要知道 ABC 的最少乘法次數，以及 DE 的最少乘法次數；...。其中，在決定 BCDE 的順序時，我們也可能需要嘗試 (BC)(DE) 的最少乘法次數，所以也會需要 DE 的最少乘法次數。因此，我們需要表格來記錄這些重複過的資訊。

我們可以將 Di, j 定義為「從第 i 個矩陣乘到第 j 個矩陣要花的最小乘法數」。所以，以 5 個矩陣相乘的狀況來說，如果能填出 D0, 4，則就代表求得最後解答。

我們先將表格初始化如下，其中對角線為 0 的原因是只有自己一個矩陣不用花費任何乘法，而下半部黑色代表這些值沒有意義，原因是不能倒著乘：

再來，對於每一個 Di, j，我們需要從下列數字當中找出最小值，其中第 i 個矩陣的維度是 pi-by-pi+1：

其中，以 Di, i+2 + Di+3, j + pi * pi+3 * pj+1為例，意義是「把這一刀切在 i+2 的話，所花的乘法次數是從 i 乘到 i+2 已經用的，加上從 i+3 乘到 j 用的，再加上合併起來要用的（第 i 個矩陣乘到第 i+2 個矩陣，維度會是 i-by-(i+3)）」。你可以發現，上述那些算式的求最小值，就相當於每一刀都切看看，然後比較一下哪一個最小。

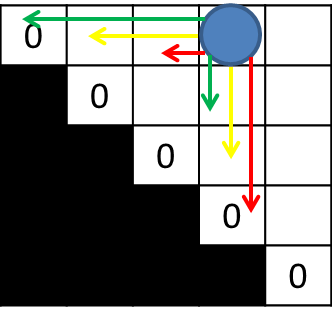
所以，以填寫 Di=0, j=3 為例，我們會需要求取下列三者的最小值：

也就是分別為下圖的綠線、黃線、紅線：

因此，填表的時候，以下兩種方向，都可以保證你在填某一格的時候，所需的資訊都已具備（當然還有其他可行的方向，但圖上並未畫出）：