如果一個函式，會呼叫到自己本身，那麼這個函式就是遞迴函式。關於遞迴，在生活中就有一些常見的例子，比如說：

從前有座山，山裡有座廟，廟裡有個老和尚，正在給小和尚講故事呢！故事是什麼呢？「從前有座山，山裡有座廟，廟裡有個老和尚，正在給小和尚講故事呢！故事是什麼呢？「從前有座山，山裡有座廟，廟裡有個老和尚，正在給小和尚講故事呢！故事是什麼呢？「從前有座山，山裡有座廟，廟裡有個老和尚，正在給小和尚講故事呢！故事是什麼呢？「 ......」」」」

或者是：

當然，對自己呼叫不會是無窮盡的，到某個條件成立時，就必須停下來，例如遞迴披薩（以披薩為配料的披薩）：

數學上也有非常多關於遞迴的式子，例如階乘的「f(1) = 1，f(n) = n * f(n-1)」，以及費氏數列的「f(1) = f(2) = 1，f(n) = f(n - 1) + f(n - 2)」等等。而遞迴在計算機科學上的定義，是將一個問題，分解成數個較小的問題求解，由小問題的解答，推出大問題的解答。雖然能用遞迴解決的問題，也都可以用迴圈解決；但有些問題，使用遞迴的方式來思考與求解，會比較直覺明瞭。但是，由於重複呼叫函式，所以遞迴容易造成系統多於的負擔，使用上必須注意。以下將用幾個簡單的範例，介紹遞迴的寫法。

雖然 Python 有內建函式可以計算階乘，但作為必須要簡單一點的第一個範例，以下將展示如何撰寫遞迴函式計算階乘：

def factorial(n):
	if n == 1:
		return 1
	return n * factorial(n - 1)


if __name__ == '__main__':
	print(factorial(5))

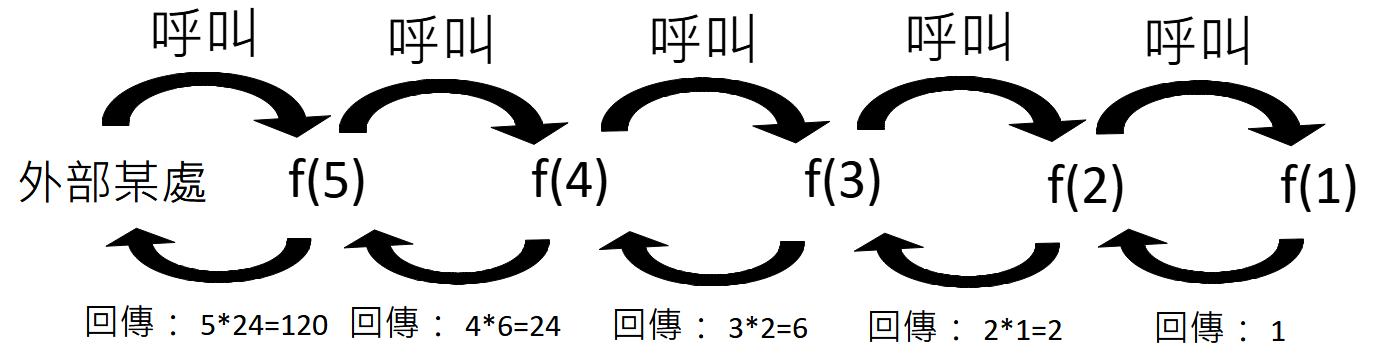
在上述範例中，第 2 及第 3 行是遞迴的終止條件，遞迴函式一定要有終止條件，否則無窮盡的呼叫，很快就會耗光系統資源。第 4 行則是對自己的呼叫，例如傳入 n = 5 時，在這行會呼叫 factorial(4)。而整個呼叫過程，可以用下圖表達：

以下程式，會用遞迴的方法計算費氏數列：

def fibonacci(n):
	if n == 1 or n == 2:
		return 1
	return fibonacci(n - 1) + fibonacci(n - 2)


if __name__ == '__main__':
	print(fibonacci(5))

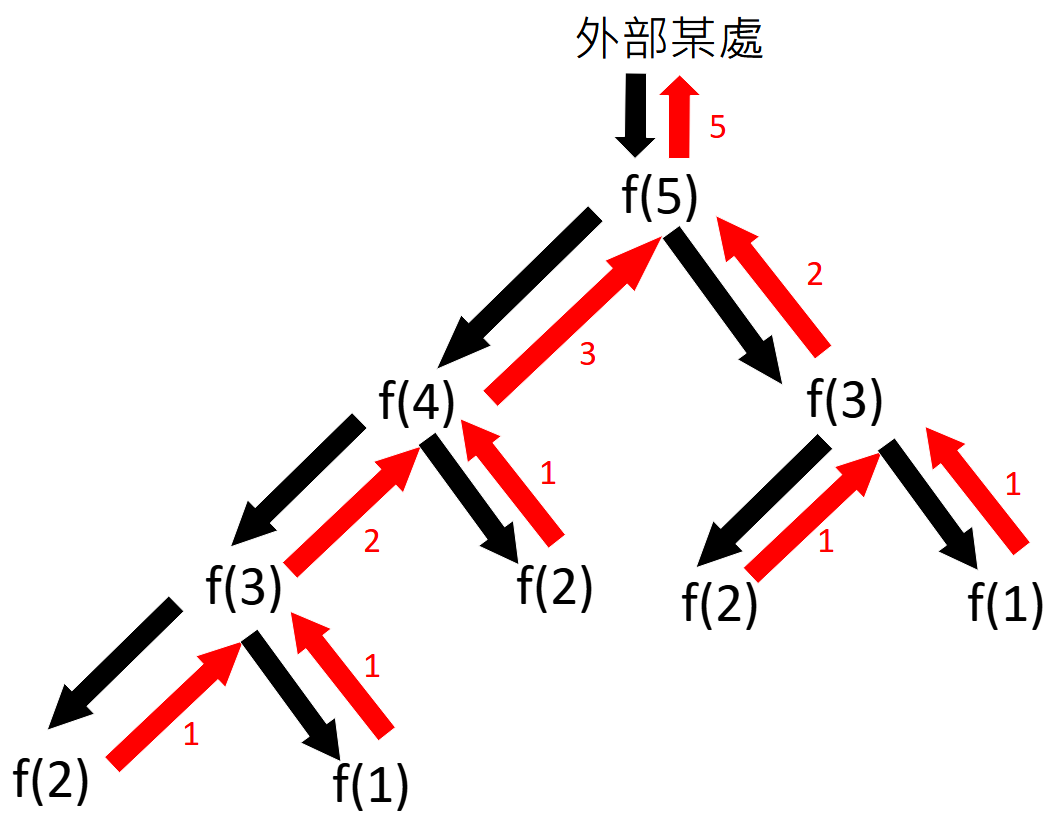
上述範例的整個呼叫過程，可以用下圖表達，其中黑色箭頭代表呼叫，紅色箭頭代表回傳，回色箭頭旁邊的數字代表該次回傳的值。順序的規則是，有黑色箭頭可以往下時就要先往下（能先呼叫就要先呼叫），左右同時有黑色箭頭時要先走左邊（加法的左右兩邊是左邊先算），黑色都走完了才能走紅色（呼叫都結束了才能回傳）：

組合個數的遞迴式為 C(m, n) = C(m - 1, n - 1) + C(m - 1, n)，亦即分成「現在這個要選」以及「現在這個不選」的兩種狀況來分別進行遞迴。撰寫成程式則如以下：

def combo(m, n):
	if n == 1:
		return m
	elif m == n or n == 0:
		return 1
	return combo(m - 1, n - 1) + combo(m - 1, n)


if __name__ == '__main__':
	print(combo(5, 3))

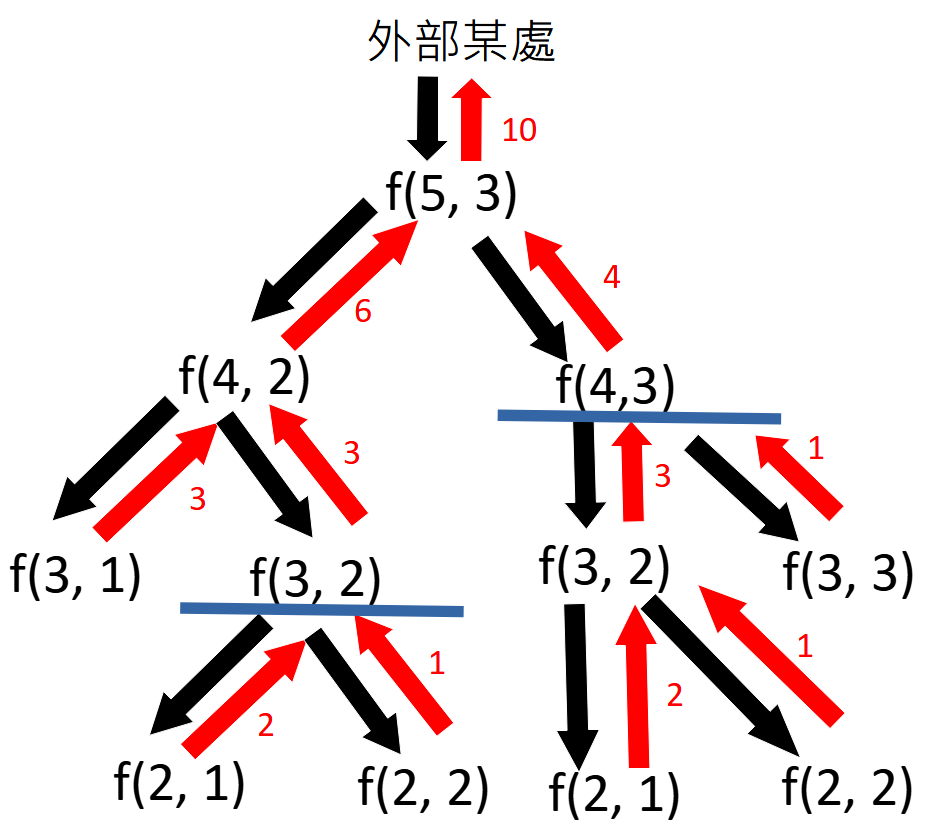
上述範例的整個呼叫過程，可以用下圖表達，圖示與上一個範例相同。你可以發現這兩個範例都有非常多部分的計算重複了，若需要使用遞迴，但是又要緩解甚至避免此種情況的話，你可以建立一個全域的串列或字典來儲存算過的內容，如果算過了就直接取用，不進行遞迴；也可以加入更多的終止條件，例如以組合個數來說，你知道當 m == n + 1 的時候有 m 種可能，就可以把這條規則也加入終止條件，則遞迴的進行就會只到下圖的藍線為止：

在 Python 當中的最大公因數（greatest common divisor, gcd）也有內建函式可以使用，但你如果會關心怎樣用遞迴自己寫的話，則可以使用 gcd(a, b) = gcd(b, a % b) 這個遞迴式來撰寫，其實就是我們以前都學過的輾轉相除法，如下：

def gcd(a, b):
	if b == 0:
		return a
	return gcd(b, a % b)


if __name__ == '__main__':
	print(gcd(100, 60))

河內塔也很容易用遞迴求解。例如在兩個盤子的情況下，你可以這樣做（假設左邊的柱子為起始點）：

1. 把小盤搬到中間（暫存柱）
2. 把大盤搬到右邊（目標柱）
3. 把小盤也搬到右邊，完成

因此，對於遞廻來說，只要把上面範例的小盤子，當成 n-1 個小盤子就好了。這個意思是說，我們可以把問題拆解成 1 個大盤子和 n-1 個比較小的盤子，至於 n-1 個小盤子的搬法，就交給遞迴解決。整體的步驟如下：

1. 把 n-1 個盤子，從「起始柱」移到「暫存柱」
2. 把第 n 個盤子移到「目標柱」
3. 把「暫存柱」的那 n-1 個盤子移到「目標柱」

def hanoi(n, start_rod, temp_rod, target_rod):
	if n > 0:
		hanoi(n-1, start_rod, target_rod, temp_rod)
		print('Move dish {} from rod {} to rod {}'.format(n, start_rod, target_rod))
		hanoi(n-1, temp_rod, start_rod, target_rod)


if __name__ == '__main__':
	hanoi(3, 1, 2, 3)